How to Go From “I Hate Math” to “I Love Math!”
Do you want your child to go from “I hate math” to “I love math?” Do you want them to have that teacher – the one that makes it so fun, so attainable – that it changes their entire attitude? My friend Lynn is one of those remarkable teachers, the kind you and your child will always remember.
Lynn has been teaching math at various grade levels for over 25 years and still lights up when she talks about what’s happening in her classroom. Lynn is also one of those rare individuals that teach in such a way, everyone in the class ‘gets it’. And if they don’t, she’ll go the extra mile to be sure they do.
So what’s her secret to teaching math this way? It’s all about teaching ‘concept before computation’ and using manipulatives. Lynn is very adept at using both sides of her brain. And as much as she understands the whole left-brain, right-brain conversation – it doesn’t factor into the way she teaches – meaning, she doesn’t think about what lefties and righties need, she just teaches in a way that works for everyone. This is an excerpt from my book, Being Visual, in which Lynn describes her success teaching math concepts first before getting bogged down with the computation. Please enjoy the read! And see if the concept and visuals make you feel a lot better about your days learning the Pythagorean Theorem.
“After 21 years of teaching math at various grade levels, I have found students are much more successful when math is first taught conceptually and then taught the procedural number crunching associated with that concept. Students are able to move on to more advanced math application and concepts when they have a solid conceptual foundation. When this process is reversed and students learn computation without theory, it is extremely difficult for them to go back and grasp the conceptual meaning later.
One of my favorite concepts to teach is the Pythagorean Theorem. It is a brand new topic and students have no prior experience, hence no misconceptions to correct. When teaching math concepts, I use a highly visual tactile approach. I have found this essential to my students’ understanding. I also feel they are more engaged and the learning “sticks”. Once students visually understand the Pythagorean Theorem, they make fewer computation errors. Conversely, a colleague who taught the Pythagorean Theorem formula first without a visual picture, noticed his students making errors because they didn’t understand the underlying theory. He tried to go back and teach the visual representation, but it seemed to just confuse his students. Another colleague, a special education teacher, introduced the theory conceptually and visually, as I did, and had tremendous success when the students later used the formula to compute.
Before introducing the Pythagorean Theorem, I must be sure students understand square numbers. To do this, each student receives a bag of colored 1-inch square tiles, and are told to make a square with the tiles. As I roam around the room, I see students who have selected one tile, others who have created a 2×2 square, a 3×3 square, etc. But surprisingly, I also see students who have created a variety of rectangles. After posing questions to help students remember the attributes of a square, they make the needed adjustments and soon all students have illustrated a square. As students share their squares with their classmates, we discuss the areas of their squares: 22 or 4 tiles, 32 or 9 tiles, 42 or 16 tiles, etc. When I explain to the students that they have created a visual representation of a square number using the colored squares, it is a light bulb moment. For years, they have heard “two squared, three squared, etc.,” but they hadn’t made the connection between the words and a visual picture!
With this understanding of squares, they’re ready to apply the concept of square numbers to the Pythagorean Theorem. To do this, every student receives a right triangle with legs that are 4 inches and 3 inches long with the task of trying to determine the length of the third side called the hypotenuse. This is the first time that the students are introduced to the Pythagorean Theorem formula: a2 + b2 = c2. I ask the students to illustrate a2 and b2 using the square tiles. They use 16 square tiles to make a square off the 4-inch leg, and 9 square tiles to make a square off the 3-inch leg.
The students then realize that if a2 + b2 = c2, they can prove it is true by moving the 16 tiles from one leg and the 9 tiles from the other leg to create the square on the third side of the right triangle, which is called the hypotenuse.
When the 16 square tiles from one leg and the 9 square tiles from the other leg are moved to the third side, or hypotenuse, the 25 total tiles makes a 5×5 square. Therefore, the students have just visually proved that the sum of the squares of the two legs of a right triangle equals the square of the hypotenuse.
I have always had great success with this lesson and other visual, conceptual math lessons. I have found conceptual learning is enormously facilitated by visual tactile learning strategies and children are more successful when conceptual understanding precedes computation.”
-Lynn Pittner
Math Specialist
Davis Primary School
St. Charles, IL
Keeping things conceptual is essential for visual learners but as Lynn has seen in her experiences it can help any type of learner. In my book, Being Visual, I address what makes visual learners unique and give many ideas and ways for you to help your child succeed in a left-brain world.
For more ideas on how to focus on the concepts rather than the computation take a look at Make Your Visual Kid a Math Whiz . Are you looking for some great math apps to keep the kids busy at the doctor’s office?

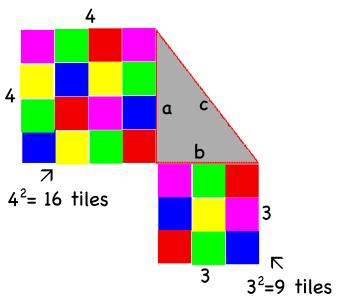 With this understanding of squares, they’re ready to apply the concept of square numbers to the Pythagorean Theorem. To do this, every student receives a right triangle with legs that are 4 inches and 3 inches long with the task of trying to determine the length of the third side called the hypotenuse. This is the first time that the students are introduced to the Pythagorean Theorem formula: a2 + b2 = c2. I ask the students to illustrate a2 and b2 using the square tiles. They use 16 square tiles to make a square off the 4-inch leg, and 9 square tiles to make a square off the 3-inch leg.
With this understanding of squares, they’re ready to apply the concept of square numbers to the Pythagorean Theorem. To do this, every student receives a right triangle with legs that are 4 inches and 3 inches long with the task of trying to determine the length of the third side called the hypotenuse. This is the first time that the students are introduced to the Pythagorean Theorem formula: a2 + b2 = c2. I ask the students to illustrate a2 and b2 using the square tiles. They use 16 square tiles to make a square off the 4-inch leg, and 9 square tiles to make a square off the 3-inch leg. 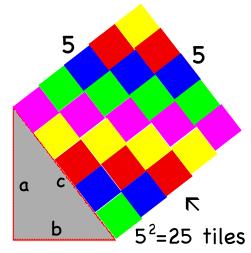 When the 16 square tiles from one leg and the 9 square tiles from the other leg are moved to the third side, or hypotenuse, the 25 total tiles makes a 5×5 square. Therefore, the students have just visually proved that the sum of the squares of the two legs of a right triangle equals the square of the hypotenuse.
When the 16 square tiles from one leg and the 9 square tiles from the other leg are moved to the third side, or hypotenuse, the 25 total tiles makes a 5×5 square. Therefore, the students have just visually proved that the sum of the squares of the two legs of a right triangle equals the square of the hypotenuse.
